Papers and preprints

Joint with Jordan Ellenberg, David Plaza, José Simental, and Geordie Williamson. Inspired by permutations suggested by AlphaEvolve (an evolutionary coding agent developed by Google DeepMind), we discover massive hypercubes inside the Bruhat order of the symmetric group. This phenomenon has consequences for cluster algebras, Kazhdan–Lusztig theory, and moduli spaces of embeddings of Bruhat graphs, and provides a striking example of how AI can contribute to genuine mathematical discovery. From a mathematical point of view, the result is beautiful: the Bruhat interval defining this massive hypercube is described by a purely number-theoretic condition on permutations, a behavior completely unlike anything we had previously seen.

Joint with Gastón Burrull and Rodrigo Villegas. In this paper, we show that classifying Bruhat intervals (up to poset isomorphism) is not the nightmare it first appears to be. Our proof may not win a beauty contest :) but the result itself turns out to be surprisingly simple and elegant.

Joint with Ben Elias, Hankyung Ko and Leonardo Patimo, to appear in Revista Matemática Iberoamericana. This is the fifth paper on the development of a diagrammatic singular Hecke theory. Here we introduce a generalization of the twisted Leibniz rule for the Demazure operator associated to any atomic double coset. This is equivalent to a polynomial forcing property for singular Soergel bimodules.

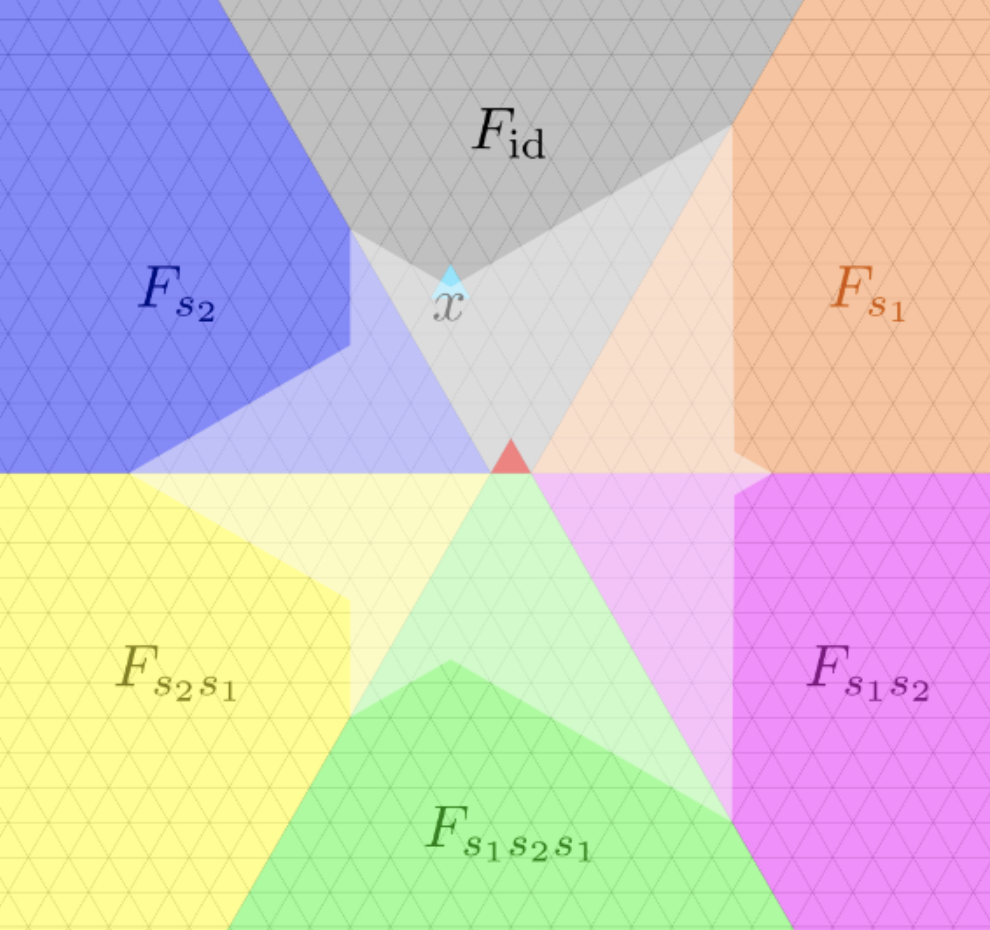
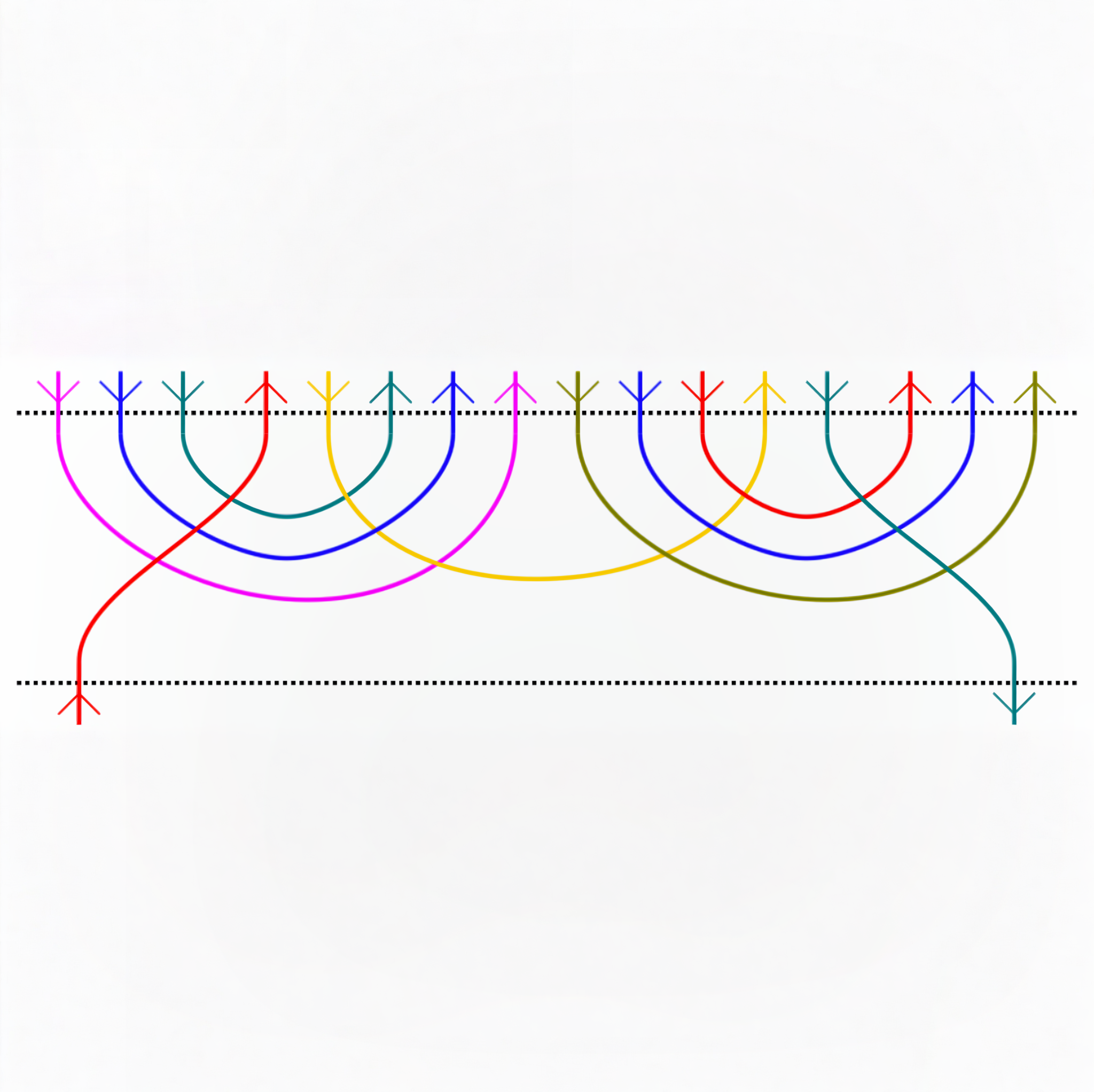
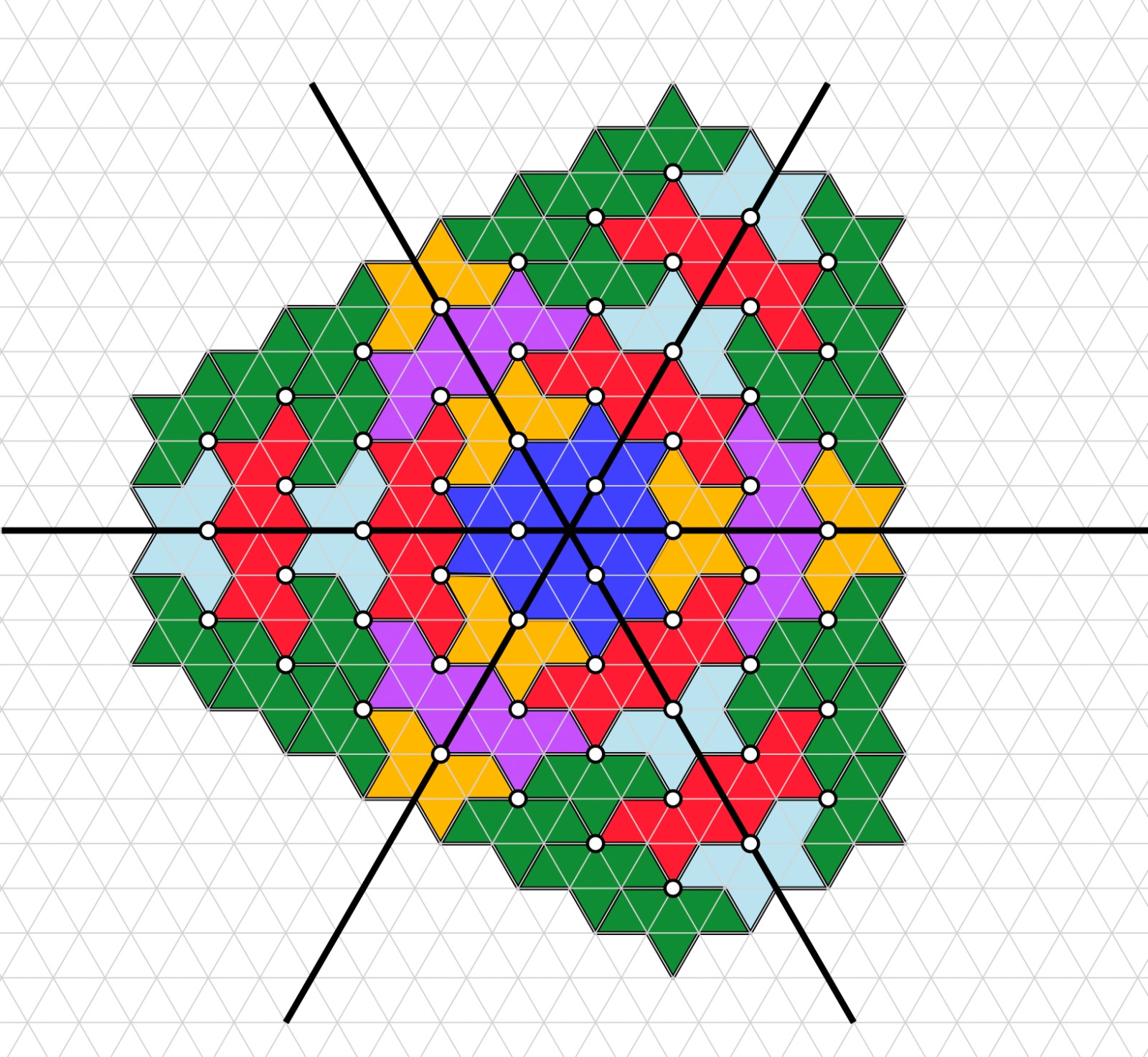
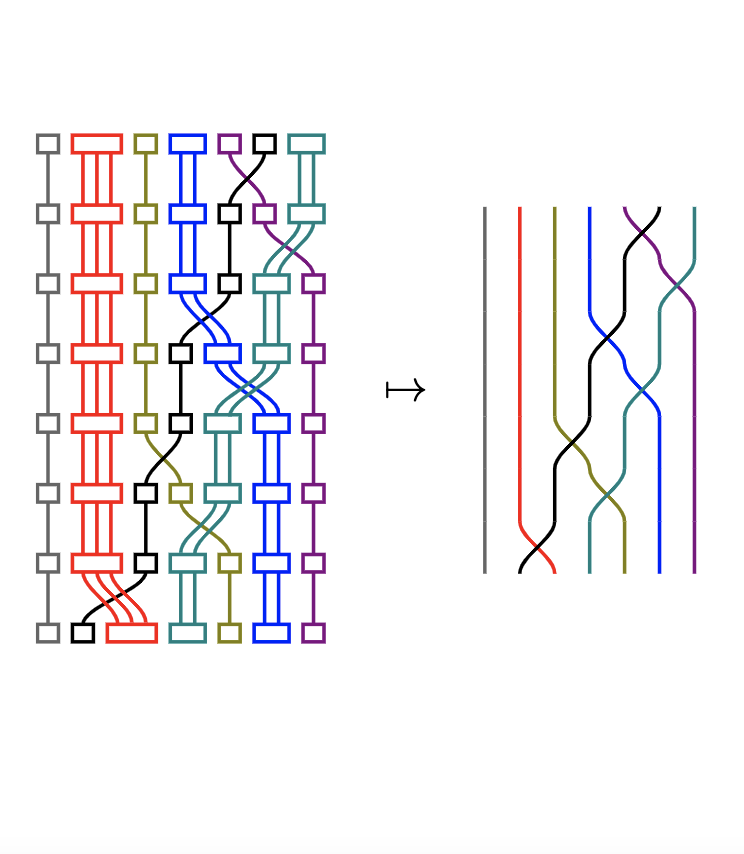
Joint work with Federico Castillo, Damian de la Fuente, and David Plaza. We introduce the notion of a Paper Boat: a new combinatorial object that tessellates the lower intervals of elements in the lowest two-sided Kazhdan–Lusztig cell. Using Paper Boats and convex geometry, we obtain formulas for the cardinalities of these intervals and show that they are given by (quasi-)polynomials. We further conjecture that, in fact, they are always genuine polynomials. As a byproduct of this work, we also discovered a natural partition of the group that is particularly well adapted to studying polynomiality, and which appears to have interesting applications in its own right.

Joint with Ben Elias, Hankyung Ko and Leonardo Patimo, to appear in Mathematical Research Letters. We produce an algorithmic construction of a reduced expression for any double coset.

Joint with Federico Castillo, Damian de la Fuente and David Plaza. For affine Weyl groups and elements associated to dominant coweights, we give a convex geometry formula for the size of the corresponding lower Bruhat intervals (this says in particular that it is a polynomial in several variables). Extensive computer calculations for affine Weyl groups have led us to believe that a similar formula exists for all lower Bruhat intervals. We also believe that the cardinality of all Bruhat intervals is given by some family of quasi-polynomials.

Joint with Leonardo Patimo, Selecta Mathematica 29 (2023), no. 4, Paper No. 64. We find a surprisingly beautiful basis of the Hom spaces between indecomposable Soergel bimodules for SL(3) (something that we call indecomposable light leaves.

Accepted for publication in Journal of the Indian Institute of Science 102, No. 3, 907-946 (2022). It is an introduction/survey of representation theory with lots of humor, open questions, and extremely smart insights :)

Joint with Gastón Burrull and David Plaza, International Mathematics Research Notices 10 (2023) 8903–8933.  We prove the combinatorial invariance conjecture (by G. Lusztig and M. Dyer in the eighties) for the affine A2. This is the first infinite group with non-trivial Kazhdan-Lusztig polynomials where this fascinating conjecture is proved.

Joint with Leonardo Patimo and David Plaza, Advances in Mathematics  399 (2022). For any affine Weyl group, we introduce the pre-canonical bases, a set of bases of the spherical Hecke algebra that interpolates between the standard basis and the canonical basis. Thus we divide the hard problem of calculating Kazhdan-Lusztig polynomials (or q-analogues of weight multiplicities) into a finite number of much easier problems.